新聞やテレビなどで「指数関数的に増える」という表現が使われることがあります。さて、この「指数関数」とはどのようなものなのでしょうか。日本に昔からある「ねずみ算」から考えてみましょう。
1、ねずみ算の例
塵劫記(じんこうき)という江戸時代の算術書があります。その問題の中に「ねずみ算」が登場します。
<問題>
正月にネズミの夫婦が現れて12匹の子供を生んだ。そのうち半数がメスだった。
2月には母親と6匹のメスの子供がそれぞれ12匹の子供を生んだので、全部で98匹になった。
メスは毎月12匹の子供を生み、その半分がメスである。生まれたネズミも親も死なないとして、12月には何匹になっているでしょう?
1月に12匹生み、2月には98匹になると書いてあるので、おそらく12月にはもっと増えるだろうことはわかりますね。問題文のように計算すると、1月のねずみは2+12=14匹となり、2月のねずみは2+12+84=98匹です。(図1参照)
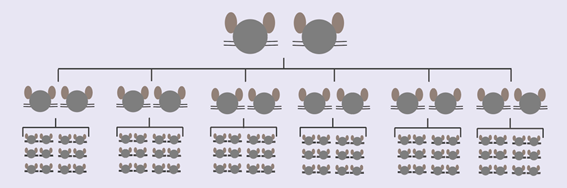
図1 2月までのネズミの数
3月以降も同様に考えると、14、98、686・・と1か月毎に7倍ずつ増えていくため、12月には
2×7×7×7×7×7×7×7×7×7×7×7×7=2×712
=27,682,574,402
となります。(図2参照)
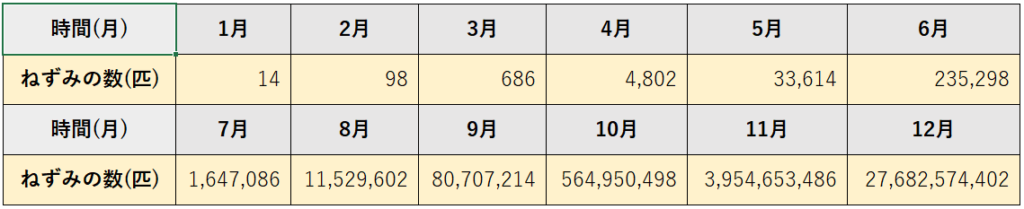
図2 12か月毎のねずみ算の計算結果
※7の右肩に小さく12と書かれている数の表現は、「7を12回かけあわせた」ことを短く書くための累乗(るいじょう)という書き方です。
このねずみ算をすると、2匹のねずみは12か月後に約270億匹に増えることがわかります。あまりにも数が大きくて想像しにくいので、増え方の様子をグラフにしてみましょう。(図3参照)

図3 ねずみ算の数の増え方の様子
グラフから、3月まではゆるやかな増加だったのが、4月から増加の割合が急に大きくなることがわかります。7月以降はグラフからはみ出てしまいますね。
実際には生まれる数のばらつきや寿命、捕食圧、住みかや食物には限りがあるため、計算通りに1年で2匹のねずみが約270億匹までに増えることはありませんが、このように少ない数から倍々に増えてあっという間に大きな数になる現象を「ねずみ算的に増える」と表現します。
2、指数関数の例
指数関数は、累乗の右肩に書かれた(ねずみ算では12となっていた)数字が変数になっているものです。これはy=axと書くことができます。(axは aのエックスじょうと読みます。)
例として、aが10の時、すなわちy=10xを考えてみましょう。
xに・・・-2,-1,0,1,2・・・と代入するとどうなるでしょう。(図4参照)

図4 y=10xの計算結果(-4から4まで)
xの値が正の方向に1変化すると、yの値は10倍の値になります。4変化すると10,000倍の値。このため、大きく変化した値まで収まるようにグラフを描くと、Xの値が1変化したときのyの値は何も変化していないように見えてしまいますね。(図5参照)
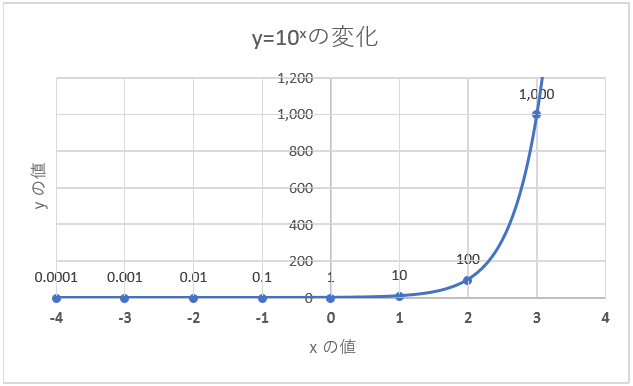
図5 y=10xの増え方の様子(Xは-4から4までの区間)
xが-4のから4まで増える間に、yの値は1億倍に増えているのに、図5のグラフでは細かい変化はつかみにくくなっています。一見変化してないように見える部分をくわしく調べるために、y=10xの変数が-1から1まで変化したときの値を見てみましょう。(図6、図7参照)

図6 y=10xの計算結果(-1から1まで)

図7 y=10xの増え方の様子(Xは-1から1までの区間)
図7のように、-1から1までの短い区間でも、指数関数のグラフは右側にいくと急に変化が大きくなっていることがわかります。
ニュースなどで見かける「指数関数的に」という表現は、増加の割合が極めて大きいことを意味しています。もし、この表現がでてきたら、繰り返しの頻度(ひんど)や増加の割合に注目してみてください。
例えば、病気にかかった人の数が、ある時点から爆発的に増えるのは、1人の感染者から数人に感染することが繰り返されるという現象に、「指数関数的」な関係性が見いだせるためかもしれません。
3、さいごに
日本の昔話に「指数関数的な」エピソードが登場するものがあります。
この「倍々とんち話」は米粒にまつわるお話ですが、今までの解説を参考に、どのような数になるか計算してみてください。
豊臣秀吉に好きな褒美を与えると言われた曽呂利新左衛門(そろりしんざえもん)は、1日目は1粒、2日目は2粒、3日目は4粒のように100日間にわたって、倍々の米をもらいたいと言いました。さて、100日後に曽呂利新左衛門は何粒の米をもらえるでしょうか?
ヒント:豊臣秀吉は曽呂利新左衛門の希望をかなえることはできなかったそうです。













