2021年8月7日(土)に伊藤 由佳理先生を講師にお招きし、夏の特別企画展の関連イベントとしてオンライン講演会「『美しい数学』から見える世界」を開催しました。
本イベントでは、講師の問いかけに対し参加者からチャットを通じ多くのコメントがあり、活発なコミュニケーションが行われました。ここでは一部内容をダイジェストとしてご紹介します。
なお、紹介した数学の詳しい説明につきましては、伊藤 由佳理著「美しい数学入門」(岩波書店)もあわせてご覧ください。
講師:伊藤 由佳理(東京大学カブリ数物連携宇宙研究機構 教授)
0、はじめに
数学の美しさを定義するのは難しいですが、数学者は「あるものの集まりに共通の性質を見つける」、「規則性」、「対称性」、「一般化・高次元化」、「対応」等に注目し、これらに美しさを感じています。

1、分類する:仲間外れをつくらない方法
服を引き出しに入れるときに、同じ形、同じ色などに分けて入れることができます。このように、同じ引き出しに入る関係を同値関係といいます。「AとBは同値である」をA~Bと書きます。(~はチルダと読む)
同値関係~は次のルールをみたす
- X~X
- X~YならY~X
- X~YかつY~ZならばX~Z
同値関係になる例は、色、形、学年、年齢、出身地、身長などです。同値関係にならない例は、性格、顔、知り合い、仲良しなどです。学校で行われる班分けで、仲良し同士で集まるのがうまくいかないことがあるのは、「仲良し」が同値関係ではないためです。仲間外れにならないように分けるには同値関係を使って考えるのが良いでしょう。
問1 上の例以外に、同値関係になる例と、同値関係にならない例を考えてみましょう。
2、いろいろな幾何学:偏見をなくそう!
「三角形の内角の和は180度」はいつでも正しいか?という問いかけを考えてみると、平面上に描いた三角形では常に成り立ちます。小学校から高校までに習うユークリッド幾何学では、角度や長さが大切です。
しかし、球面上に描いた、最短距離で結んだ線(測地線)を辺とする三角形の内角の和は180度以上になります。鞍面に描いた三角形の内角の和は180度未満になります。このような「三角形の内角の和は180度」が成り立たない世界を考えるために新しい幾何学が生まれました。
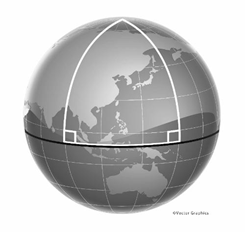
地球儀の表面上の三角形の例
三角形の点をそれぞれA,B,Cとし、最短距離で各点をつなぐと、その曲率は
(∠A+∠B+∠C)-180°
と書けます。微分幾何学はこの曲率で分類する幾何学です。アインシュタインは曲率の考え方を用いて相対性理論を組み立てました。
位相幾何学では、穴の数に注目します。例えば、鉄道の駅名が並ぶ路線図は地図上の位置関係を省略して描くことが多く、位相幾何学の発想が用いられています。
このように普段使っているユークリッド幾何学以外にも色々な幾何学があり、場合によっては正しかった性質も成り立たなくなることがあります。
問2 球の表面上で、測地線で作られた三角形の内閣の和が最大となる三角形はどのようなものでしょうか。
3、対称性:規則性を見つける
規則性がある図形には対称性があります。「対称性をもつ」とは、ある操作(合同変換)をした後に初めの状態と同じ状態になることを指し、数学的に表したものを「群」と呼びます。
家紋は「回転」や「裏返し」といった操作ができる群として捉えることができます。異なるデザインでも操作が同じ場合は、対応する群は同じです。

家紋の例(出典:Wikipedia)
「回転」や「裏返し」に「平行移動」を加えると、壁紙のように連続する図形が得られます。図形を自分自身に重ねる動かし方は2次元結晶群と呼ばれ、17種類あることが知られています。3次元結晶群は230種類あり、自然界の中でその結晶群に分類できる物質を見つけることができます。4次元では4783種類知られていますが、5次元以上はまだわかっていません。数学者は、高次元化や抽象化したらどうなるだろうと考えることがあります。
対称性は、自然科学の中でも見出せます。例えば、
- 野依良治氏による、鏡像異性体が存在する分子を触媒によって作り分ける「不斉分子触媒の開発」。
- 小林誠氏と益川敏英氏による、粒子と反粒子の非対称性を理論的に予想し、約30年後に加速器実験で実証された「CP対称性の破れの起源の発見」。
などです。自然科学と数学ではアプローチの仕方が異なります。
数学は、答えは一つですが考え方はひとつではありません。色々な考え方をすることが大事です。
自然科学は、答えがたくさんある場合もありますが、調べる方法は大抵一通りで、その中から色々なことを見出すことが多いです。
問3 身の回りにある「対称性をもつ」モノを探してみましょう。
4、まとめ
最後は、伊藤先生の研究について紹介します。
研究の対象は代数幾何学、特に「特異点」です。その物理現象の例としてはブラックホールやビッグバンが挙げられます。超弦理論では、宇宙は10次元の空間で、時空(4次元)とカラビ・ヤウ多様体(6次元)を足し合わせたものと解釈します。伊藤先生はカラビ・ヤウ多様体に関連する特異点を研究しています。

伊藤 由佳理氏
日常の中でも数学が使われています。例えば、インターネット検索、宅配便で荷物を送る、電車の乗換案内、データサイエンス・ビッグデータ、AI(人工知能)、折り紙、編み物、ビーズ細工など、たくさんあります。
学校で習う算数・数学以外にも、身の回りにはたくさん数学があります。もし、自分が今まで気が付かなかった算数や数学の「気づき」や「発見」があれば、じっくり考えてみてください。そのような発見を見つけた小中高生は、算数・数学の自由研究コンクール(主催:一般財団法人 理数教育研究所)に応募することができますので、ぜひ取り組んでみてください。
数学に関する映画として、唯一の女性フィールズ賞受賞者マリアム・ミルザハニさんのドキュメンタリー映画「曲面の秘密ーマリアムの魔法の杖」があります。その日本語字幕をKavli IPMUで監修し、ウェブサイトで公開され、ダウンロード視聴できるようになりました。(有償)多くの方々に観ていただければ幸いです。
5、高柳館長のコメント
これまで多摩六都科学館の中では、数学にベースを置いた講演会はほとんどありませんでした。基礎科学のフロンティア、例えば、超弦理論は高度な数学が使われています。学校で訓練している数学以外の数学があるということを、若い人たちに小さい時から知ってもらう方が良いと思っており、この講演会がその機会になったことを喜んでいます。
分類の話で思い出したことは、以前、科学史の本を訳した際に、分類すると必ず「その他」が出てきたことでした。科学では「その他」を捨てる立場と、「その他」を大事に取っておいて後からきれいに拾う立場があり、科学の歴史でもこのような分類をしてきていたのです。
数学が持つ分類の機能を用いて、分類することで美しさに気づくこともあります。物理学の世界では対称性をきれいに使って、ある操作をしても不変量があることから法則を導いたり、チェックしたりしています。
科学と同様に、数学は文化であり、人間の営みの中で、基本的で重要な世界の見方を提供してくれます。今回は色々な世代の方に知ってもらう機会となりました。伊藤先生、ありがとうございました。













